Contour following and profile estimation

Three different experiments have been performed to test the contour following algorithm.

The first one concerns the measurement of a linear profile with an artificial burr (Figs. 1-2).

Fig. 1

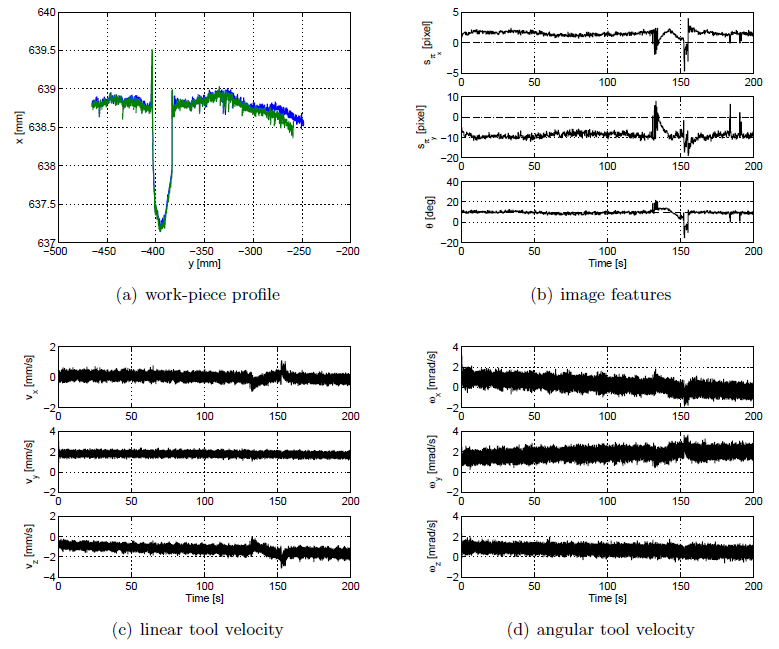
Fig. 2

Fig. 3

The two other experiments show the performance of the contour following system in the case of a complex profile. In this case a work-piece with a profile characterised by a sequence of arcs of different radius has been selected (Fig. 3). The two experiments concern the contour following of the bigger and the smaller arc that characterise the work-piece. Though the geometry of the profile is more complex than in the first experiment, the control system exhibits almost the same performance (Fig. 4).

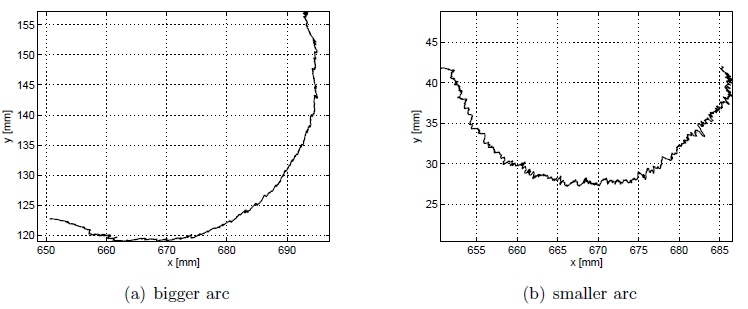
Fig. 4

The performance of the second part of the system, i.e. the triangulation algorithm, has been assessed in a realistic scenario, measuring the changes in the burr profile during a sequence of seven deburring trials. The experiment was organised as follows. First, different measurements of similar profiles have been taken and the nominal profile has been reconstructed. Then, the nominal profile has been used to drive the robot through seven different deburring trials, changing the depth of cut in the range from 0 to 1 mm (Figs. 5-6).

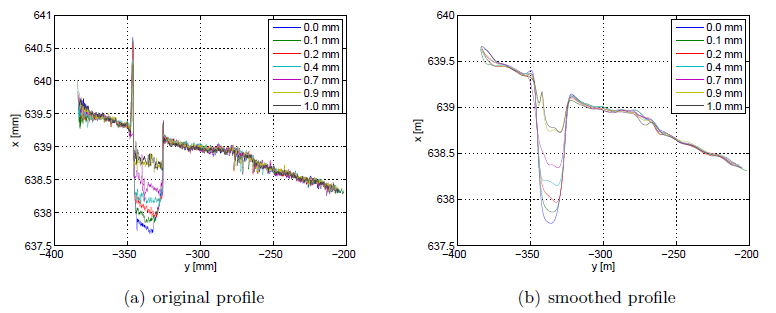
Fig. 5

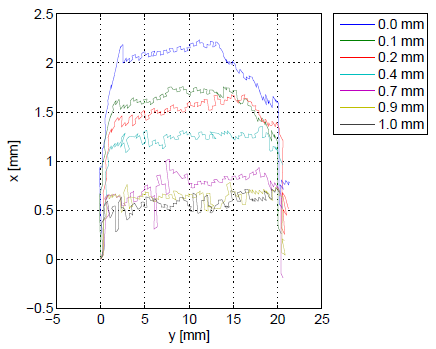
Fig. 6

Learning the tool path

Once a set of profiles of different work-pieces, characterised by the same nominal profile but affected by different burrs, has been acquired, the profiles are transformed into the distance space and a mean (or a median) profile is computed. The rationale behind this procedure is that if burrs are randomly distributed along the profiles of the different work-pieces, and if burr dimensions are negligible with respect to the work-piece dimensions, the mean profile approximates, with good accuracy, the nominal one.

An algorithm to generate a synthetic burr dataset has been developed. Interpolating the profiles reported in Figs. 6 and extracting the heigh of each point belonging to the actual profile with respect to the nominal one, seven models of burrs with the same length but different heights and a model of a segment of profile without burrs have been generated (Fig. 7).

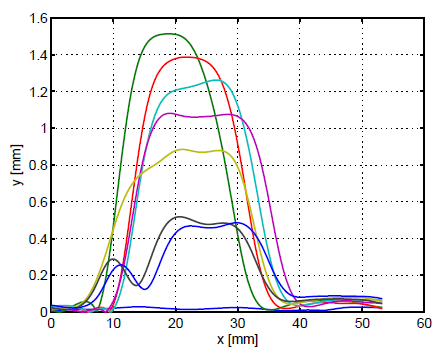
Fig. 7

Two different sets, each one composed of ten synthetic profiles, have been generated. The first one, reported in Fig. 8, is based on a linear nominal profile, the second one, shown in Fig. 9, on a circular nominal profile. The learning path procedure was applied to both sets, giving rise to the results reported in Figs. 10-11.

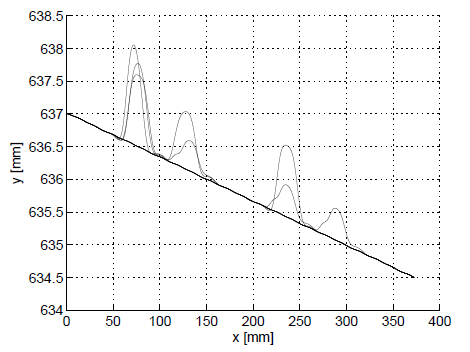
Fig. 8

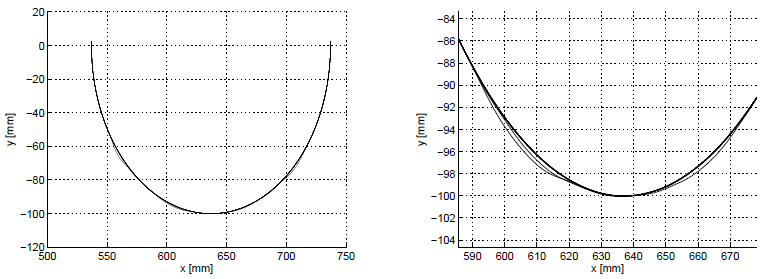
Fig. 9

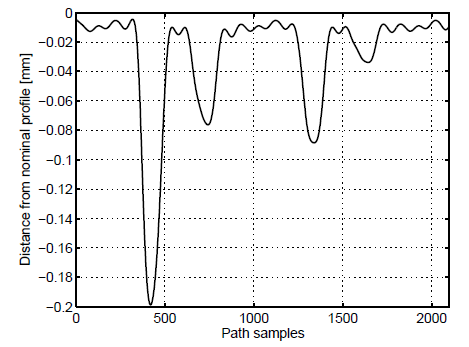
Fig. 10

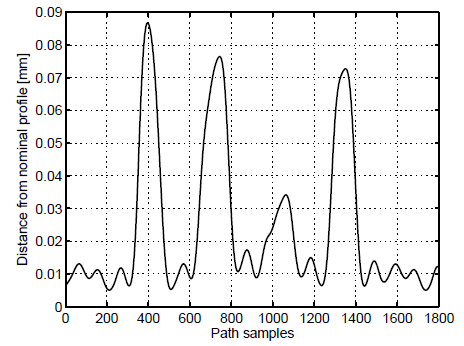
Fig. 11