Contour following and profile estimation

Three different experiments have been performed to test the contour following algorithm.

The first one concerns the measurement of a linear profile with an artificial burr (Figs. 1-2).

Fig. 1

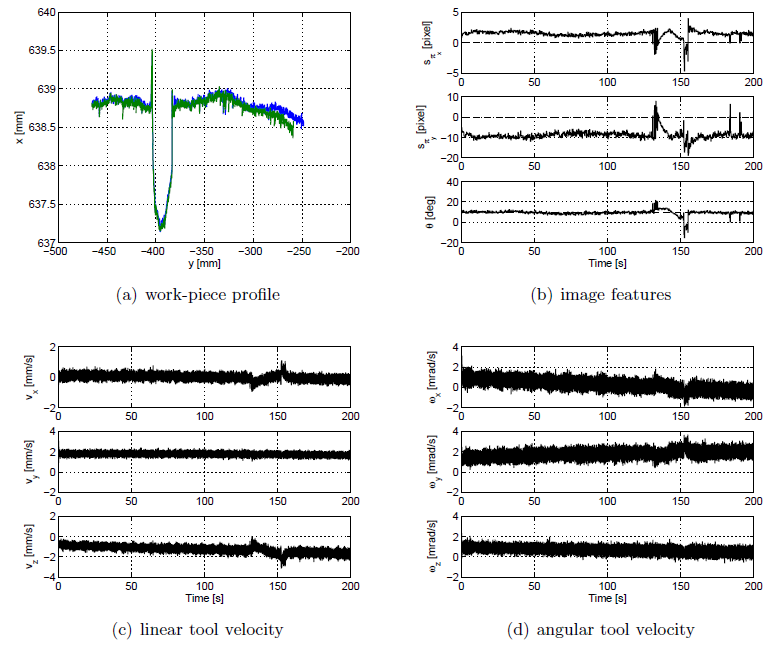
Fig. 2

Fig. 3

The two other experiments show the performance of the contour following system in the case of a complex profile. In this case a work-piece with a profile characterised by a sequence of arcs of different radius has been selected (Fig. 3). The two experiments concern the contour following of the bigger and the smaller arc that characterise the work-piece. Though the geometry of the profile is more complex than in the first experiment, the control system exhibits almost the same performance (Fig. 4).

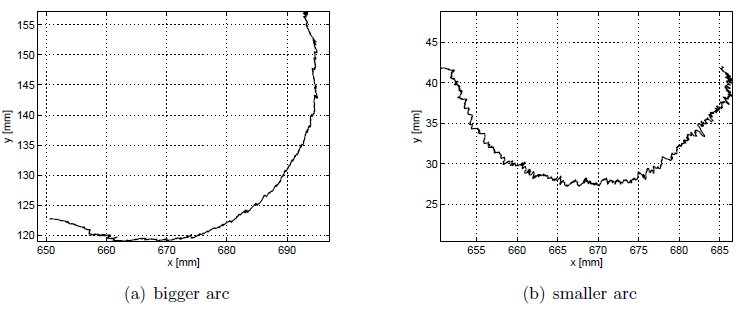
Fig. 4

The performance of the second part of the system, i.e. the triangulation algorithm, has been assessed in a realistic scenario, measuring the changes in the burr profile during a sequence of seven deburring trials. The experiment was organised as follows. First, different measurements of similar profiles have been taken and the nominal profile has been reconstructed. Then, the nominal profile has been used to drive the robot through seven different deburring trials, changing the depth of cut in the range from 0 to 1 mm (Figs. 5-6).

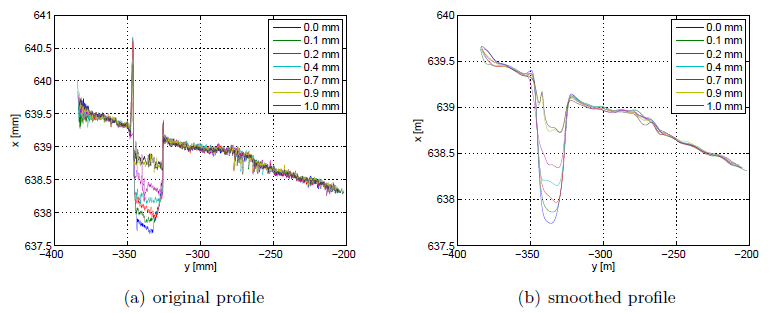
Fig. 5

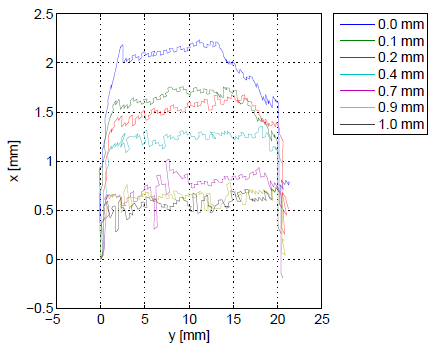
Fig. 6

Learning the tool path

Once a set of profiles of different work-pieces, characterised by the same nominal profile but affected by different burrs, has been acquired, the profiles are transformed into the distance space and a mean (or a median) profile is computed. The rationale behind this procedure is that if burrs are randomly distributed along the profiles of the different work-pieces, and if burr dimensions are negligible with respect to the work-piece dimensions, the mean profile approximates, with good accuracy, the nominal one.

An algorithm to generate a synthetic burr dataset has been developed. Interpolating the profiles reported in Figs. 6 and extracting the heigh of each point belonging to the actual profile with respect to the nominal one, seven models of burrs with the same length but different heights and a model of a segment of profile without burrs have been generated (Fig. 7).

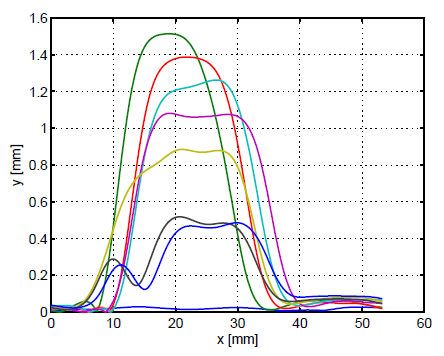
Fig. 7

Two different sets, each one composed of ten synthetic profiles, have been generated. The first one, reported in Fig. 8, is based on a linear nominal profile, the second one, shown in Fig. 9, on a circular nominal profile. The learning path procedure was applied to both sets, giving rise to the results reported in Figs. 10-11.

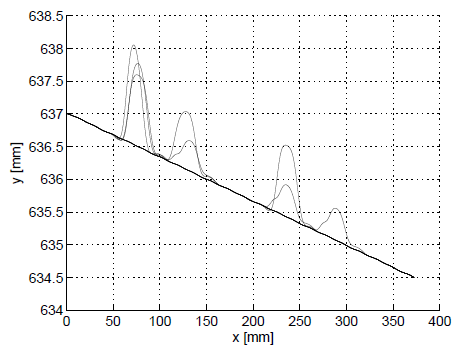
Fig. 8

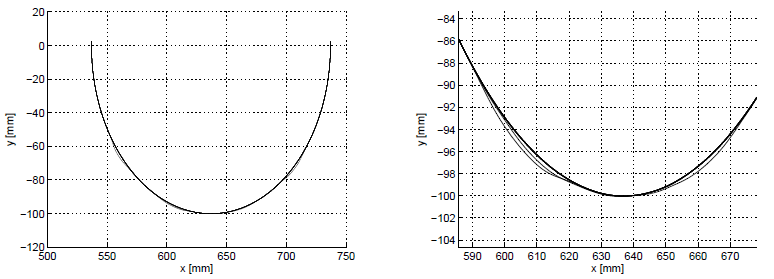
Fig. 9

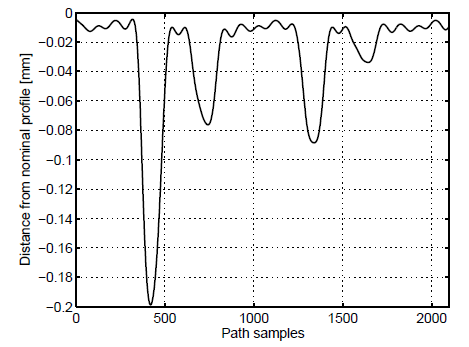
Fig. 10

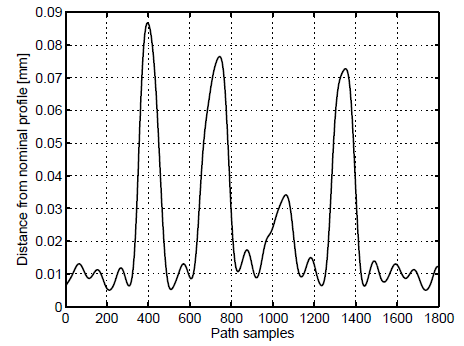
Fig. 11

Walk-through programming
The problem of walk-through programming in contact with an hard surface is still under studying.
The main concerns are related to the implementation of a robust algorithm to detect the contact and estimate the normal to the surface.

Wheel localisation and burr analysis
To localise the wheel a camera mounted on top of the working area is usually adopted. Further, in industrial applications the valve hole is the feature usually adopted to localise the wheel. Nevertheless, we decided to mount the camera on the robot shoulder considering the following advantages:

• it is a simpler and more compact solution, that does not require any additional frame to support the camera (that could represent a dangerous obstacle in the robot workspace);
• it allows for a bigger and less occluded field of view (we do not need to ensure that the arm does not occlude the wheel or the valve hole);
• the shoulder camera can be used as an additional sensor during the deburring operation or as a recording device.

The shoulder mountig, however, entails disadvantages as well: the majority of the time the valve hole is occluded or difficult to detect due to shadows or poor illumination. The pictures taken by the camera from different robot positions suggest that the bolt holes (and their positions with respect to the wheel) represent a set of robust features to localise the wheel.

Concerning burr analysis, it must be noticed that the burr profile is estimated directly on the image plane (no extrinsic camera parameters need to be calibrated). Nonetheless, a calibration of the laser with respect to the camera and a validation of the system precision are of upmost importance.

The following tables show the results of this validation.
Each table compares the results obtained with two algorithms, A e B, and the one computed as the mean of the previous ones. In algorithm A the position of each point of the laser line is determined looking for the point, along a perpendicular to the laser, that maximises the brightness. On the other hand, algorithm B determines the position of the points on the line as the mean value between an upper and a lower threshold on the derivative of the brightness.

The first table concerns measurements of the distance along the z (focal) axis of the camera frame, between the center of the camera frame and the surface of a calibration object, a stair of 9 steps, each with an height of 1 cm.
Mean and standard deviation were computed processing 100 pictures, taken with slightly different light conditions.
The table shows a very low variance in the measurements. It must be noticed, however, that there are small errors in the distances (the nominal distance between two consecutive steps is 1 cm) due to the fact that the distance between the camera and the laser was not corrected with an accurate calibration.

The last table shows the z distances measured on a part of the wheel. In this case there is no ground truth, but the small standard deviations demonstrate that accurate measures can be obtained even on a rough metal surface.

Walk-through programming
The programming mode has been realised through a set of admittance controllers.

It must be noticed that the tests reaveal that the classical implementation of the walk-through programming mode does not allow for motion in contact with a surface. It turns out that realising the walk-through programming in contact with a hard surface (with a single force/torque sensor) is a quite challenging operation, but it is also uf upmost importance not only for this project but, for example, in many surgical robotics applications. We are still studying this problem.

Wheel localisation and burr analysis
A set of specifications for the two camera systems (one for wheel localisation, the other one for burr analysis) has been identified. Within the end of the month two cameras and a laser stripe will be available for thesting the image processing algorithms.

Some mechanical devices that can artificially mimic a contour with a burr have been also sketched and will be soon realised (see the picture below).